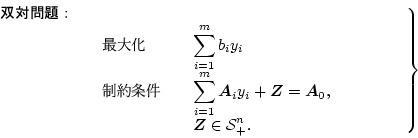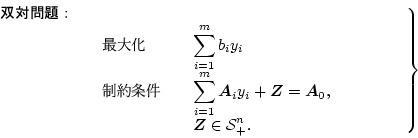半正定値計画問題

半正定値計画問題（はんせいていちけいかくもんだい、英: semidefinite programming）とは、半正定値行列全体によって作られる凸錐体上での凸最適化問題（convex optimization）の一つである。

半正定値計画問題は近年いくつかの理由で成長している最適化の一分野である。その理由として多くの実用例が考えられることがあげられるが、特にオペレーションズ・リサーチや組み合わせ最適化などの分野で広く研究が行われている。自動制御理論の分野では半正定値計画問題が線形不等式制約のもとで行われることが多い。半正定値計画問題は、凸錐体上の凸最適化問題の一種であり、内点法などにより効率よく解を与えることが可能であることも、応用が期待される一要因となっている。また半正定値計画問題の階層化により多項式最適化問題が近似的に解けるほか、複雑系の最適化にも応用が可能である。

定義

線形計画問題はある空間上で多面体に含まれるような実数の組に対して、線形の目的関数を最小化・最大化する問題である。ここで、多面体というのは、より厳密には凸集合であるということを指す。一方で、半正定値計画問題においては、ベクトルの内積を最適化する。特に、一般的な半正定値最適化問題は、数理計画問題の形式として、以下のように定義される（ただし、${\displaystyle x_{i}\cdot x_{j}}$は内積を表す）。

${\displaystyle {\begin{array}{rl}{\displaystyle \min _{x^{1},\ldots ,x^{n}\in \mathbb {R} ^{n}}}&{\displaystyle \sum _{i,j\in [n]}c_{i,j}(x^{i}\cdot x^{j})}\\{\text{subject to}}&{\displaystyle \sum _{i,j\in [n]}a_{i,j,k}(x^{i}\cdot x^{j})\leq b_{k}\qquad \forall k}.\\\end{array}}}$

さらに、この問題は半正定値行列の作る凸錐体上の問題として書き直すことができる。大きさが ${\displaystyle n\times n}$ の行列 ${\displaystyle M}$ が ${\displaystyle n}$ 本のベクトル ${\displaystyle x^{1},\ldots ,x^{n}}$ を用いて ${\displaystyle m_{i,j}=x_{i}\cdot x_{j}}$ で表されるとき、行列${\displaystyle M}$をグラム行列といい、この行列は半正定値となることが知られている。

ここで、${\displaystyle \mathbb {S} ^{n}}$を実対称行列全体の空間とする。この空間では内積を ${\displaystyle \langle A,B\rangle _{\mathbb {S} ^{n}}={\rm {tr}}(A^{T}B)=\sum _{i=1,j=1}^{n}A_{ij}B_{ij}}$ （ただし、tr は行列の跡を表す）と定義することができて、これを用いると、前述のベクトルを用いた半正定値計画問題が次の形で書き直せる。

${\displaystyle {\begin{array}{rl}{\displaystyle \min _{X\in \mathbb {S} ^{n}}}&\langle C,X\rangle _{\mathbb {S} ^{n}}\\{\text{subject to}}&\langle A_{k},X\rangle _{\mathbb {S} ^{n}}\leq b_{k},\quad k=1,\ldots ,m\\&X\succeq 0\end{array}}}$

ただし、${\displaystyle X\succeq 0}$ とは行列 ${\displaystyle X}$ が半正定値行列であることを表す。この式において ${\displaystyle C}$ は ${\displaystyle c_{i,j}}$ を、${\displaystyle A_{k}}$ は ${\displaystyle n\times n}$ の行列で ${\displaystyle a_{i,j,k}}$ を成分に持つ。

双対性

双対問題の定義

線形計画問題と同様、半正定値計画問題も双対問題を考えることが可能で、

${\displaystyle {\begin{array}{rl}{\displaystyle \min _{X\in \mathbb {S} ^{n}}}&\langle C,X\rangle _{\mathbb {S} ^{n}}\\{\text{subject to}}&\langle A_{k},X\rangle _{\mathbb {S} ^{n}}\leq b_{k},\quad k=1,\ldots ,m\\&X\succeq 0\end{array}}}$

という半正定値計画問題の双対問題は

${\displaystyle {\begin{array}{rl}{\displaystyle \max _{y\in \mathbb {R} ^{m}}}&\langle b,y\rangle _{\mathbb {R} ^{m}}\\{\text{subject to}}&{\displaystyle \sum _{i=1}^{m}}y_{i}A_{i}\preceq C\end{array}}}$

という形で与えられる。なお大きさが等しい2つの正方行列 ${\displaystyle P,Q}$ に対して、${\displaystyle P\succeq Q}$ とは、${\displaystyle P-Q\succeq 0}$ と同義である。

弱双対性

弱双対定理とは、半正定値計画問題の主問題と双対問題の許容解の関係を表す定理であり、主問題の許容解が双対問題の上界となり、双対問題の許容解が主問題の下界となるというものである。 これは、次の式により示される。

${\displaystyle \langle C,X\rangle -\langle b,y\rangle =\langle C,X\rangle -\sum _{i=1}^{m}y_{i}b_{i}=\langle C,X\rangle -\sum _{i=1}^{m}y_{i}\langle A_{i},X\rangle =\langle C-\sum _{i=1}^{m}y_{i}A_{i},X\rangle \geq 0,}$

最後の不等式が成立するのは、行列の内積を取っている2つの行列が、どちらも半正定値行列であるためである。

強双対性

スレーター条件と呼ばれる条件の下では、主問題と双対問題の最適解が一致することが知られている。これを強双対性という。線形計画問題と違い、半正定値問題は、すべての問題が強双対性を満たすわけではなく、一般には双対問題の最適解は主問題の最適解よりも小さい。強双対性は次の2つの性質により言い表される。

1. 主問題が下に有界であり、かつ内点許容解をもつとき、双対問題が最適解${\displaystyle y^{*}}$を持つ。
2. 双対問題が上に有界であり、かつ内点許容解をもつとき、主問題が最適解${\displaystyle X^{*}}$を持つ。

この2つの性質から、主問題と双対問題の両方が最適解を持ち、それらが一致することが言える。

参考文献

• 田村明久, 村松正和, 『最適化法』, 共立出版株式会社, pp. 176-194, 2002年.