置換積分

微分積分学において置換積分（ちかんせきぶん, 英語: Integration by substitution）は、変数変換を用いて積分を計算する積分法である。

一変数の置換

不定積分の置換積分

連続関数 f(x) と微分可能関数 x = g(t) について次の等式が成り立つ。

\int f(x)\,dx=\int f(g(t))g'(t)\,dt.

導出には以下のように連鎖律と微分積分学の基本定理を用いる。

{\begin{aligned}{\frac {d}{dt}}\int f(x)\,dx&={\frac {d}{dx}}\int f(x)\,dx\cdot {\frac {dx}{dt}}\\&=f(x)g'(t)=f(g(t))g'(t)\\&={\frac {d}{dt}}\int f(g(t))g'(t)\,dt.\end{aligned}}

この等式から変換公式の両辺の不定積分は t で微分したときに等しいことから、定数項の違いを除いて等しいことが帰結される。

また、変換公式は形式的に f(x) = f(g(t)) と dx = g'(t) dt に分けて考えることができる。後者は厳密には微分形式の理論によって正当化され、後述する多変数の置換積分と併せて積分の変数変換を一般化する。

定積分の置換積分

定積分で変数変換する際には、以下のように積分区間も変換される。

\int _{g(a)}^{g(b)}f(x)\,dx=\int _{a}^{b}f(g(t))g'(t)\,dt.

例

例1

\int _{0}^{2}x\cos(x^{2} 1)\,dx.

u = x² 1 で x から u に変数変換する。ここで、du = 2x dx なので x dx = (1/2)du である。また、x = 0 に対して u = 0² 1 = 1 であり、x = 2 に対して u = 2² 1 = 5 であるので、

{\begin{aligned}\int _{x=0}^{x=2}x\cos(x^{2} 1)\,dx&{}={\frac {1}{2}}\int _{u=1}^{u=5}\cos(u)\,du\\&{}={\frac {1}{2}}(\sin(5)-\sin(1))\end{aligned}}

と計算できる。

例2

\int _{0}^{1}{\sqrt {1-x^{2}}}\,dx.

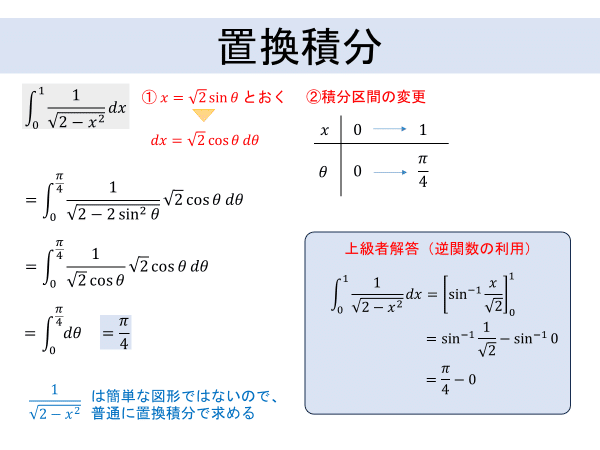
x = sin(u) で x から u に変数変換する。このとき、dx = cos(u) du である。また、0 = sin(0) および 1 = sin(π/2) であることから積分区間を [0, π/2] に変換すると、この区間において |cos(u)| = cos(u) であることに注意して、

{\begin{aligned}\int _{0}^{1}{\sqrt {1-x^{2}}}\,dx&=\int _{0}^{\frac {\pi }{2}}{\sqrt {1-\sin ^{2}(u)}}\cos(u)\,du\\&=\int _{0}^{\frac {\pi }{2}}|\cos(u)|\cos(u)\,du=\int _{0}^{\frac {\pi }{2}}\cos ^{2}(u)\,du\\&={\Bigg (}{{\frac {u}{2}} {\frac {\sin(2u)}{4}}{\Bigg )}{\Bigg \vert }\,}_{0}^{\frac {\pi }{2}}={\frac {\pi }{4}} 0={\frac {\pi }{4}}\end{aligned}}

と計算できる。

多変数の置換

x=φ(u,v),y=ψ(u,v)と変数変換すると

$\iint f(x,y)dxdy=\iint f(\phi (u,v),\psi (u,v))|J|dudv$

ここで、

$J={\frac {\partial (x,y)}{\partial (u,v)}}=\det \left({\begin{matrix}{\frac {\partial {x}}{\partial {u}}}&{\frac {\partial {x}}{\partial {v}}}\\{\frac {\partial {y}}{\partial {u}}}&{\frac {\partial {y}}{\partial {v}}}\end{matrix}}\right)$